一道关于最小磁场面积的物理题

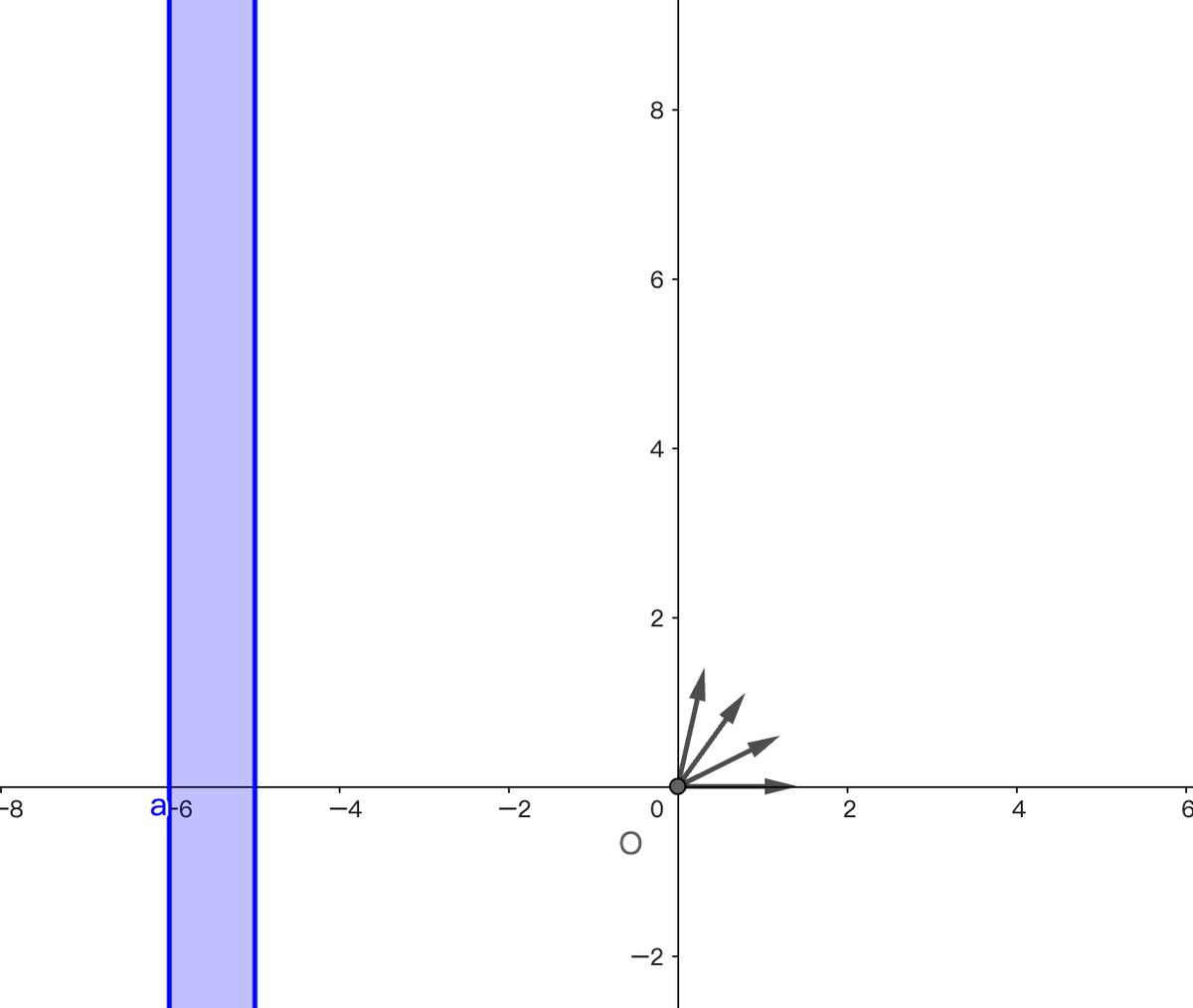
原题

如图所示，电子质量为 $m$，电荷量为 $e$，从坐标原点 $O$ 处沿 $xOy$ 平面射入第一象限，射入时速度方向不同，速度大小均为 $v_0$，现在某一区域加一方向向外且垂直于 $xOy$ 平面的匀强磁场，磁感应强度为 $B$，若这些电子穿过磁场后都能垂直射到荧光屏 $MN$ 上，荧光屏与 $y$ 轴平行，求所加磁场范围的最小面积.

构造

我们不妨设电子在磁场中作匀速圆周运动的半径为 $1$.

一个看似合理的构造很容易给出：

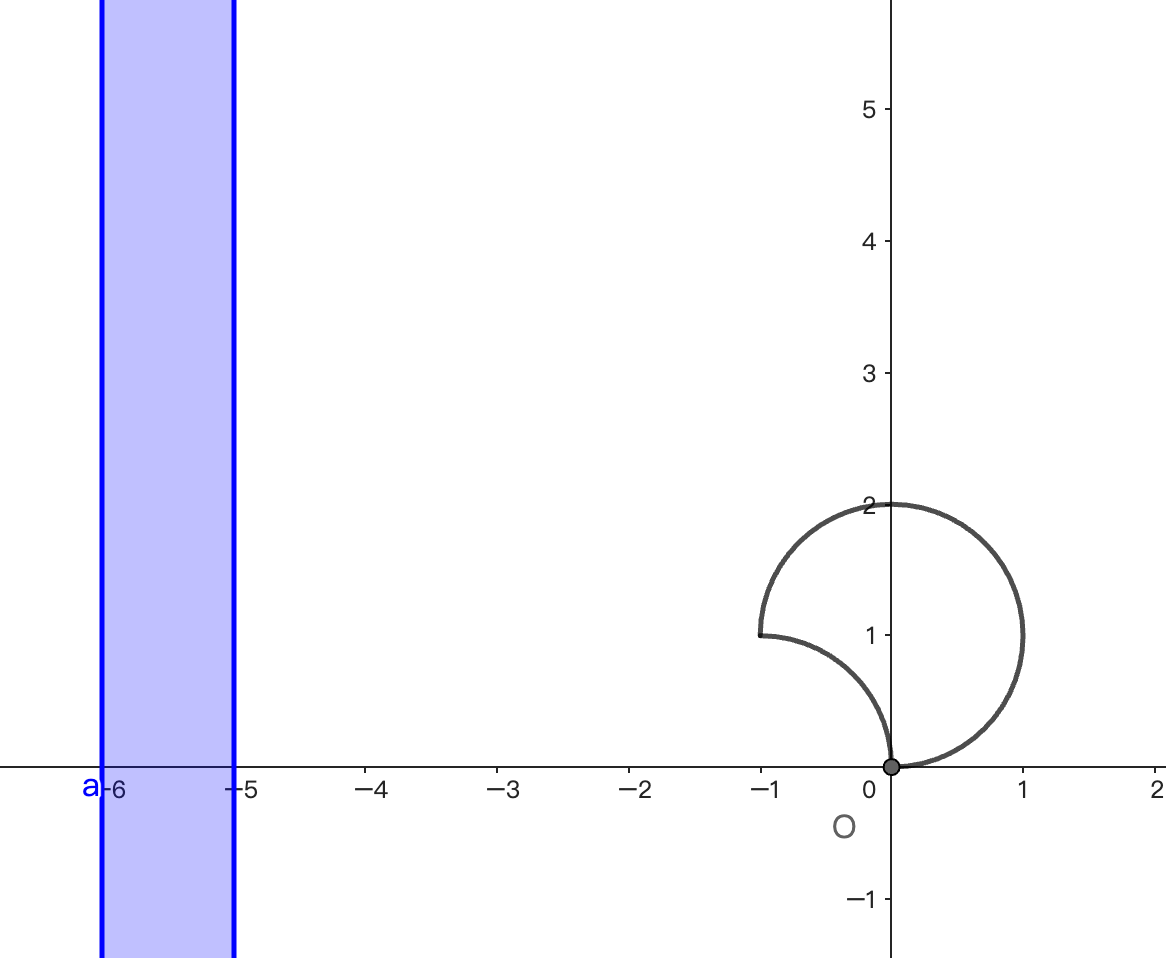
两段弧的圆心分别为 $(0,1)$ 和 $(-1,0)$，圆心角分别为 $270^\circ$ 和 $90^\circ$. 该构造得出的磁场面积为 $1+\frac{\pi}2$，刚好是原题的一个选项.

然而很容易想到这样的构造只能证明可行，却很难论证最小性. 联想到挂谷猜想，我们尝试能不能构造出面积任意小的磁场满足题设条件.

分区

首先我们将 $xOy$ 平面用倾斜角分别为 $\theta_0,\theta_1,...,\theta_n\ (\theta_0=0,\theta_n=\frac{\pi}2)$ 的直线 $l_0,l_1,...,l_n$ 分成 $n$ 个区域. 称 $l_{i-1}$ 和 $l_i$ 之间的部分记为 $A_i\ (i=1,2,...,n)$.

先考虑 $A_n$，图中绿色直线为 $l_{n-1}$，$y$ 轴为 $l_n$.

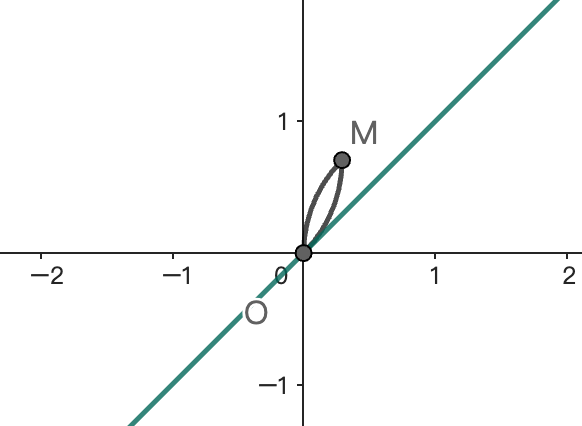
构造如图磁场，其中两个半弧半径均为 $1$，左半弧与 $l_n$ 切于 $O$，右半弧与 $l_{n-1}$ 切于 $O$. 容易得出 $A_n$ 中射出的电子经过磁场后全部方向向上，且在 $l_n$ 与过 $M$ 右半弧的切线之内.

为了将这些电子偏转到垂直打在 $MN$ 上，我们在上方另加一个磁场：

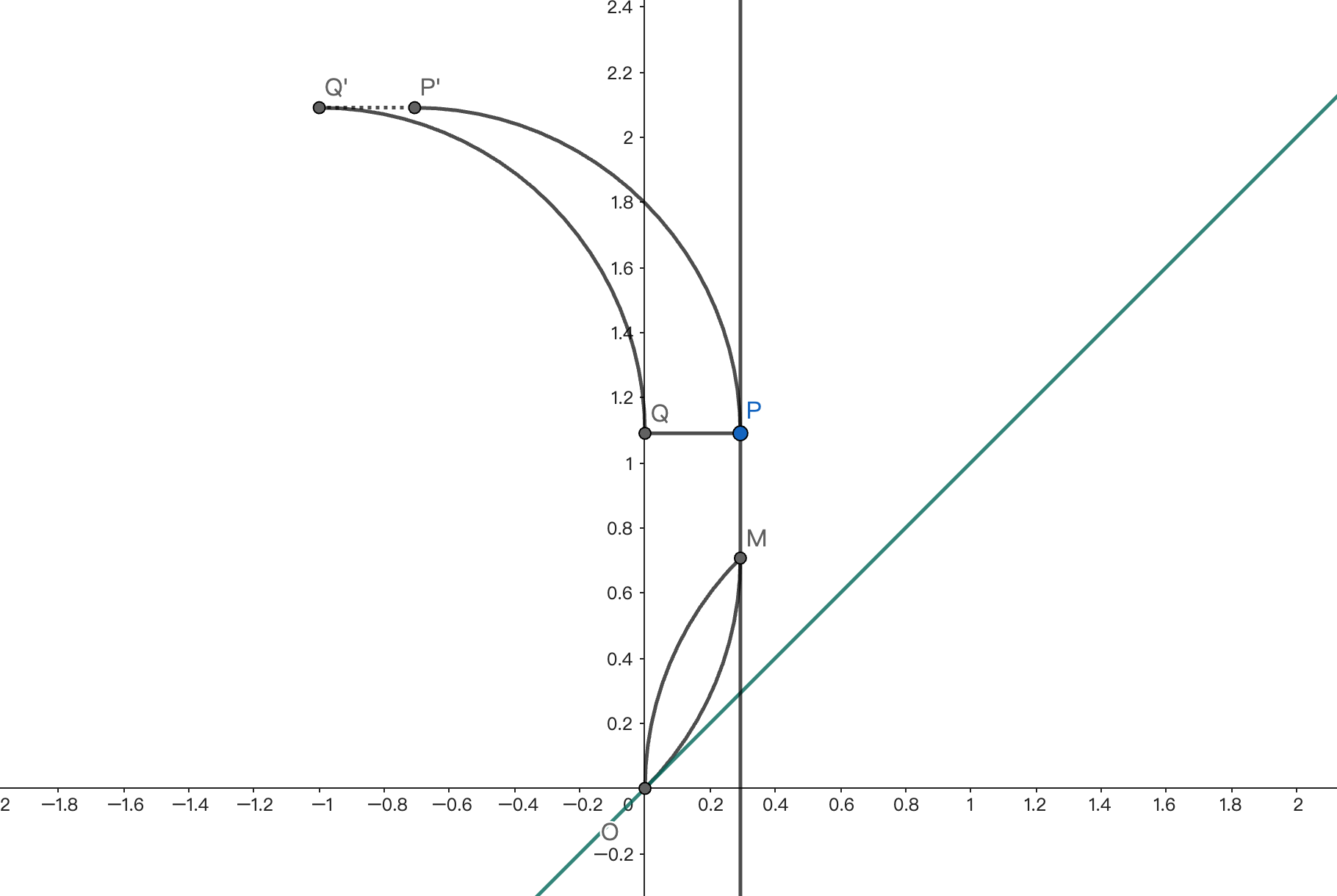
这里弧 $PP'$ 半径为 $1$，在 $P$ 点与过 $M$ 右半弧的切线相切，在 $P'$ 点切线平行于 $x$ 轴. $PQ\,//\,x$ 轴，弧 $QQ'$ 是由 $PP'$ 沿 $\overrightarrow{PQ}$ 平移得到的.

平行于 $y$ 轴射入上半磁场的所有电子都将沿着 $P'Q'$ 射出. 注意这里 $P'Q'$ 线段上是没有磁场的，不然电子会过偏转.

如此一来 $A_n$ 范围内的所有电子都能垂直打在光屏上. 以此为基础，我们从 $A_n$ 到 $A_1$ 顺次构造.

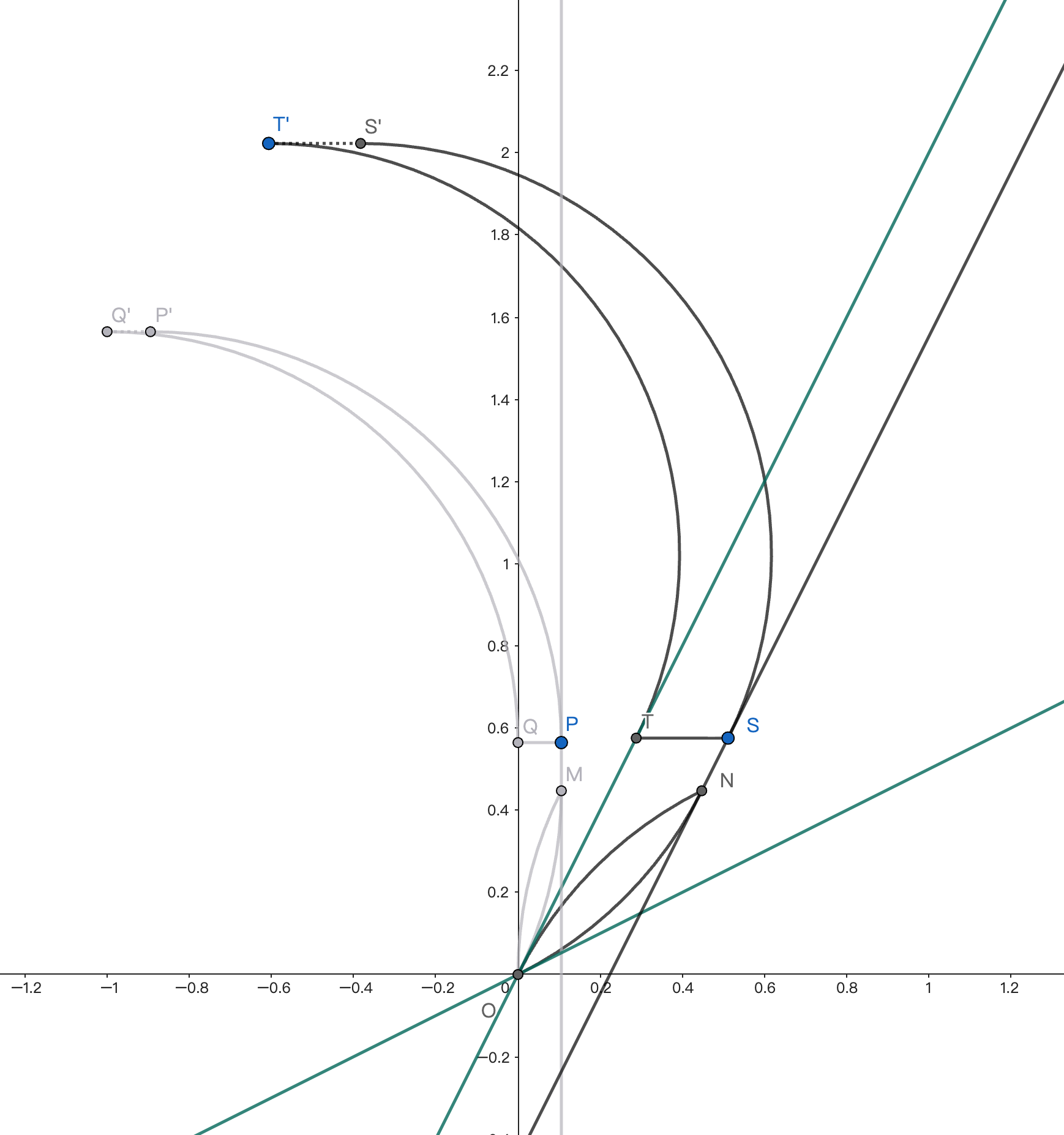
对于 $A_{n-1}$，依旧进行相同的构造，所有弧的半径依旧为 $1$，下半部分左半弧和 $l_{n-1}$ 相切，右半弧和 $l_{n-2}$ 相切. 上半部分弧线 $SS'$ 在 $S$ 点和 $l_{n-2}$ 相切，在 $S'$ 点切线平行于 $x$ 轴. $ST\,//\,x$ 轴，$TT'$ 由 $SS'$ 沿 $ST$ 平移而成.

我们可以取 $S$ 充分远使得 $A_{n-1}$ 和 $A_n$ 中电子和磁场互不干扰.

依次进行，可以构造出所有 $A_i\ (i=1,2,...,n)$ 中的磁场. 同理可得所有电子经过这样的磁场后都能垂直打在光屏上.

面积

下面求这样的磁场的面积.

对于 $A_i\ (i=1,2,...,n)$：

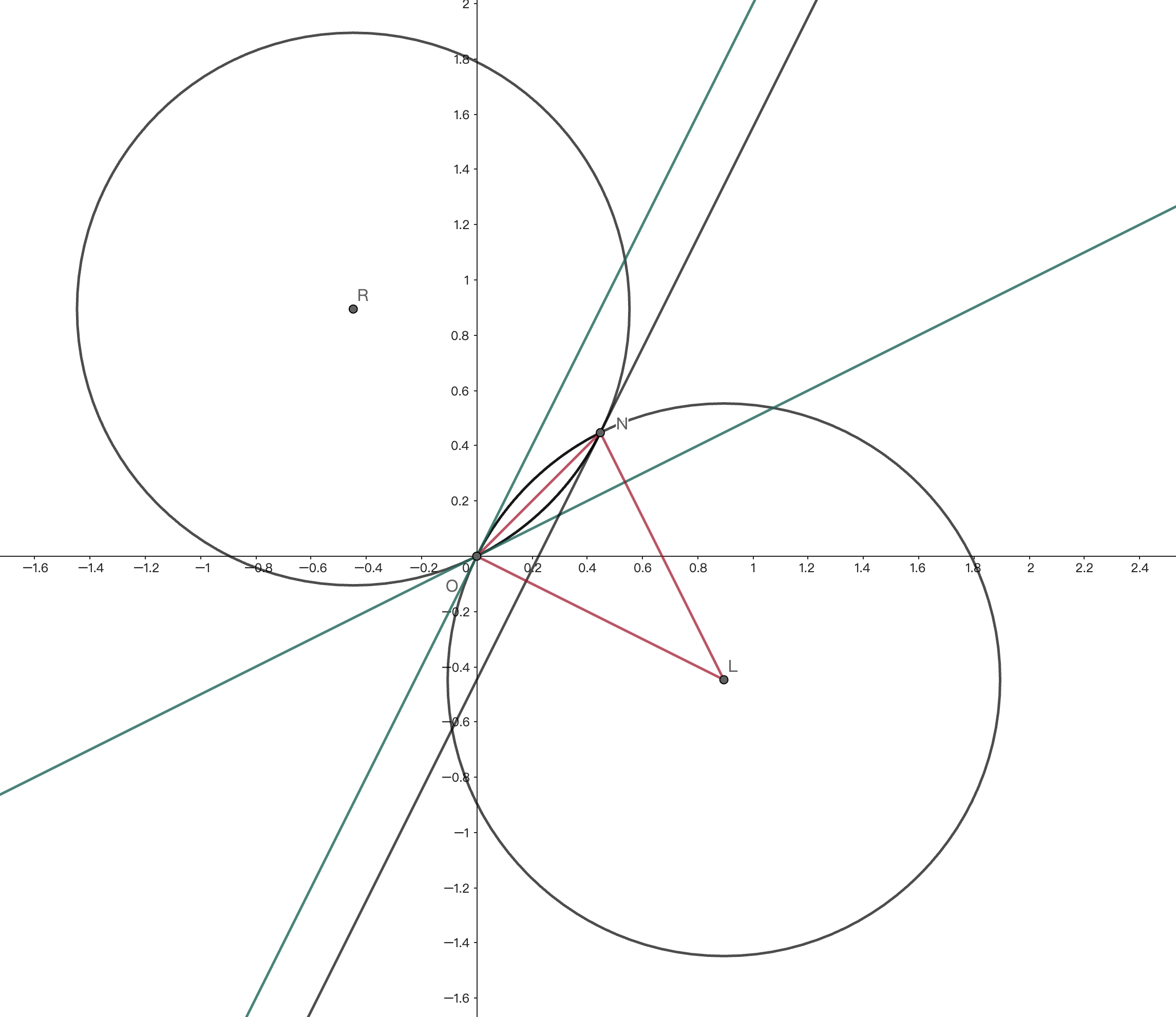
首先由弦切角，$\angle OLN=2\angle <ON,l_i>=\theta_i-\theta_{i-1}$，磁场的面积为两个全等的弓形的面积之和. 故 $S_i=2(S_{扇形LON}-S_{\triangle{LON}})=2(\frac{\theta_i-\theta_{i-1}}2-\frac{\sin{(\theta_i-\theta_{i-1}})}2)=\theta_i-\theta_{i-1}-\sin{(\theta_i-\theta_{i-1})}$.

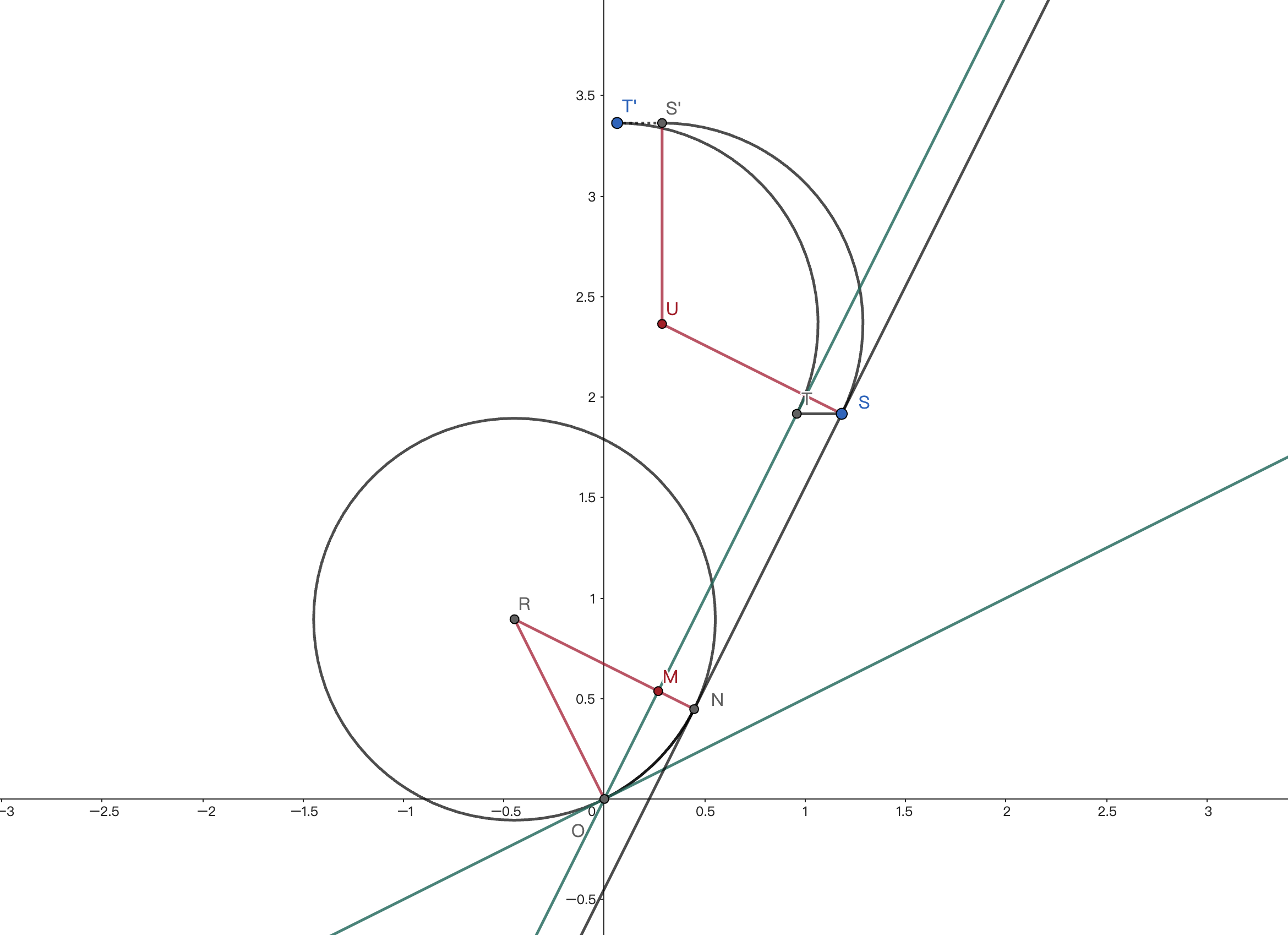
上半磁场面积利用祖暅原理转化为底($TS$)乘高($Y_{S'}-Y_S$). 我们有 $S_i'=ST\cdot(1+\cos\theta_i)\cdot US=\frac{MN}{\sin\theta_i}(1+\cos\theta_i)=\frac{1-\sin(90^\circ+\theta_{i-1}-\theta_i)}{\sin\theta_i}(1+\cos\theta_i)=\frac{1-\cos(\theta_{i}-\theta_{i-1})}{\sin\theta_i}(1+\cos\theta_i)$.

至此我们有 $S_{A_i}=S_i+S_i'=\theta_i-\theta_{i-1}-\sin{(\theta_i-\theta_{i-1})}+\frac{1-\cos(\theta_{i}-\theta_{i-1})}{\sin\theta_i}(1+\cos\theta_i)$.

极限

取 $\theta_i=\frac{i\pi}{2n}\ (i=0,1,2,...,n)$，则 $S_{A_i}=\frac{\pi}{2n}-\sin{\frac{\pi}{2n}}+(1-\cos{\frac{\pi}{2n}})\frac{1+\cos{\frac{i\pi}{2n}}}{\sin{\frac{i\pi}{2n}}}=\frac{\pi}{2n}-\sin{\frac{\pi}{2n}}+(1-\cos{\frac{\pi}{2n}})\cot{\frac{i\pi}{4n}}$.

因此所有磁场面积和为：

$$\begin{align} S_{总}&=\sum_{i=1}^{n}S_{A_i}\notag\\ &=\sum_{i=1}^{n}[\frac{\pi}{2n}-\sin{\frac{\pi}{2n}}+(1-\cos{\frac{\pi}{2n}})\cot{\frac{i\pi}{4n}}]\notag\\ &= \frac{\pi}2-n\sin{\frac{\pi}{2n}}+(1-\cos{\frac{\pi}{2n}})\sum_{i=1}^{n}\cot{\frac{i\pi}{4n}}\notag\\ &\le \frac{\pi}2-n\sin{\frac{\pi}{2n}}+(1-\cos{\frac{\pi}{2n}})(\cot{\frac{\pi}{4n}}+\int_1^n\cot{\frac{x\pi}{4n}}dx) \notag\\ &=\frac{\pi}2-n\sin{\frac{\pi}{2n}}+(1-\cos{\frac{\pi}{2n}})[\cot{\frac{\pi}{4n}}+\frac{4n}{\pi}\ln(\sin{\frac{\pi}{4}})-\frac{4n}{\pi}\ln(\sin{\frac{\pi}{4n}})] \notag\end{align}$$

取 $n$ 充分大，有：

$$\begin{align} \lim_{n\rarr+\infin} S_{总}&\le \lim_{n\rarr+\infin} \{\frac{\pi}2-n\sin{\frac{\pi}{2n}}+(1-\cos{\frac{\pi}{2n}})[\cot{\frac{\pi}{4n}}+\frac{4n}{\pi}\ln(\sin{\frac{\pi}{4}})-\frac{4n}{\pi}\ln(\sin{\frac{\pi}{4n}})]\}\notag\\&=0\notag \end{align}$$

最后一个等号由等价无穷小显然得出.

因此随着分割数的增加，磁场总面积可以小于任意一个常数. 故原题所求最小磁场其实不存在.