解析几何没解析：椭圆与圆

反演类

例1 $\odot C:(x-2)^2+y^2=4$，直线 $l_1:x+y+4=0$. $P$ 在 $l_1$ 上，以 $PC$ 为直径作 $\odot O$，求 $\odot O$ 过的所有定点.

解：

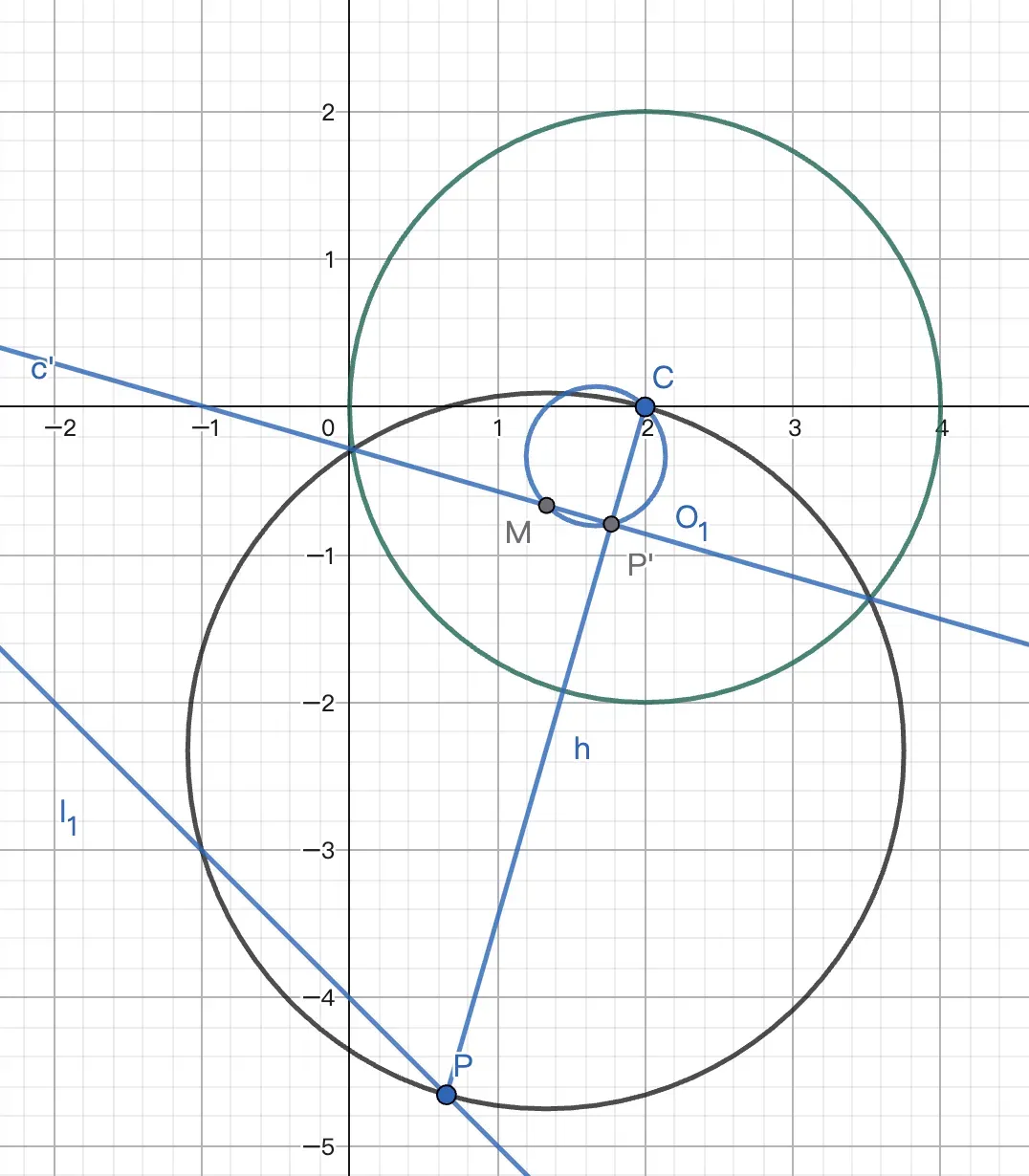
以 $\odot C$ 为反演圆，作反演变换：
$$P\rarr P'\ \odot O\rarr c'\ l_1\rarr \odot O_1$$
所以 $P'$ 在 $\odot O_1$ 上. $c'\bot CP'$. 显然 $c'$ 过 $C$ 关于 $\odot O_1$ 的对径点 $M$. 故 $\odot O$ 过 $M$ 的反点.易得 $CM:y=x-2$，联立得 $M'(-1,-3)$.

故 $\odot O$ 过定点 $(2,0),(-1,-3)$.

得到答案后，反演并非最简证法. 但它可以在不使用解析方法的情况规避看出定点在 $l_1$ 上的注意力.

例2 圆 $O_1,O_2$ 与 $x$ 轴相切且两圆圆心与原点共线. 两圆交于点 $P$，求 $P$ 到直线 $y=2x-8$ 的距离最小值.

解：

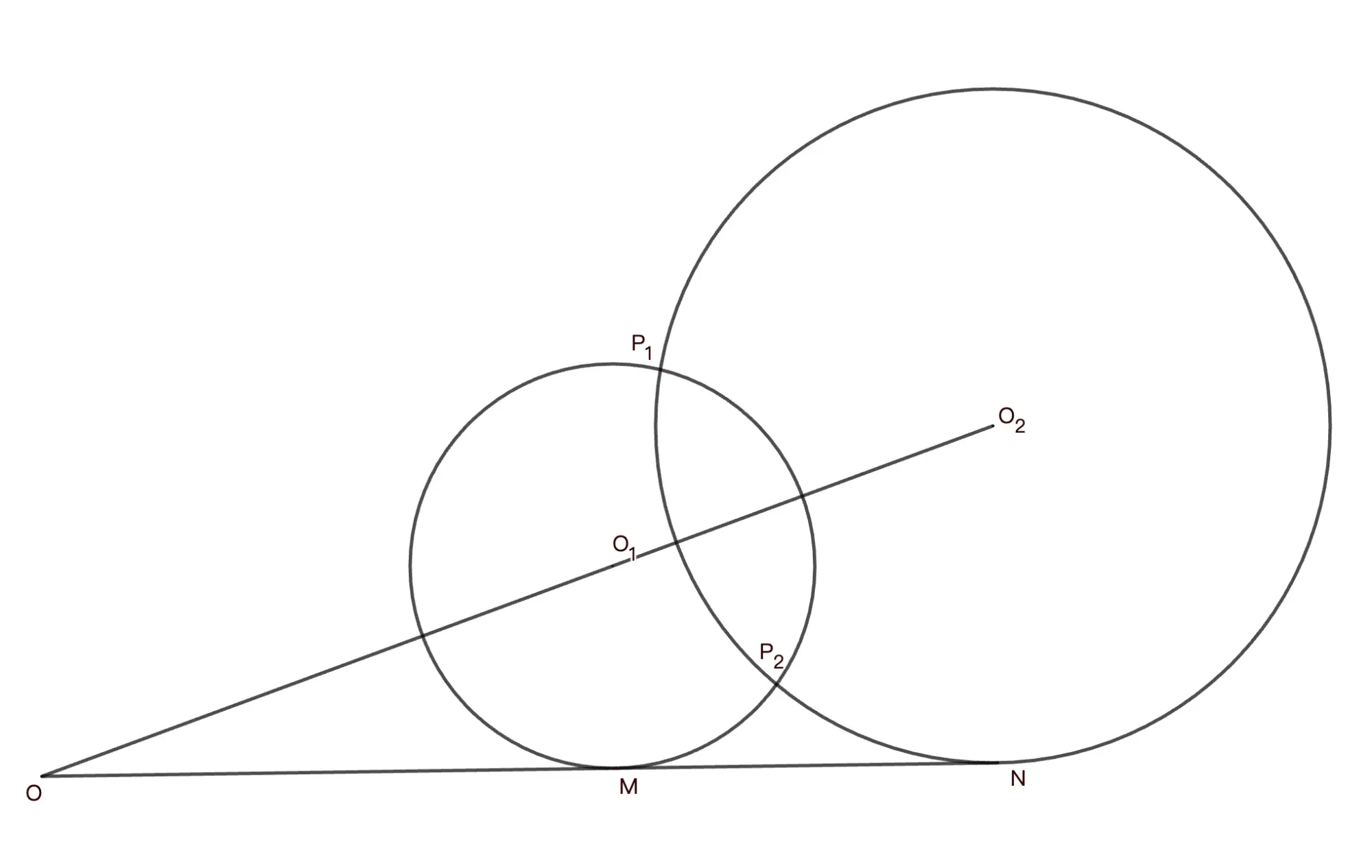
设 $\odot O_1$ 与 $x$ 轴切于 $M$，$\odot O_2$ 与 $x$ 轴切于 $N$. 以原点为反演中心，$OM\cdot ON$ 为反演幂作反演变换，则有
$$M\rightarrow N,N\rightarrow M$$
故
$$\odot O_1 \rightarrow \odot O_2\\odot O_2 \rightarrow \odot O_1$$
于是 $P\rightarrow P$，有 $OP^2=OM\cdot ON=6,OP=\sqrt{6}$.所以 $P$ 在以原点为圆心，半径为 $\sqrt6$ 的圆上.

所求最小值为 $\frac 8 5 \sqrt 5-\sqrt6$.

例3 已知圆 $C:x^2+y^2=4$ 与 $x$ 轴正半轴交于 $D$，从直线 $l:x+y=4$ 上任一动点 $P$ 向圆作切线，切点分别为 $A$，$B$，过点 $(0,1)$ 作直线 $AB$ 的垂线，垂足为 $H$，求 $DH$ 的最小值.

解：

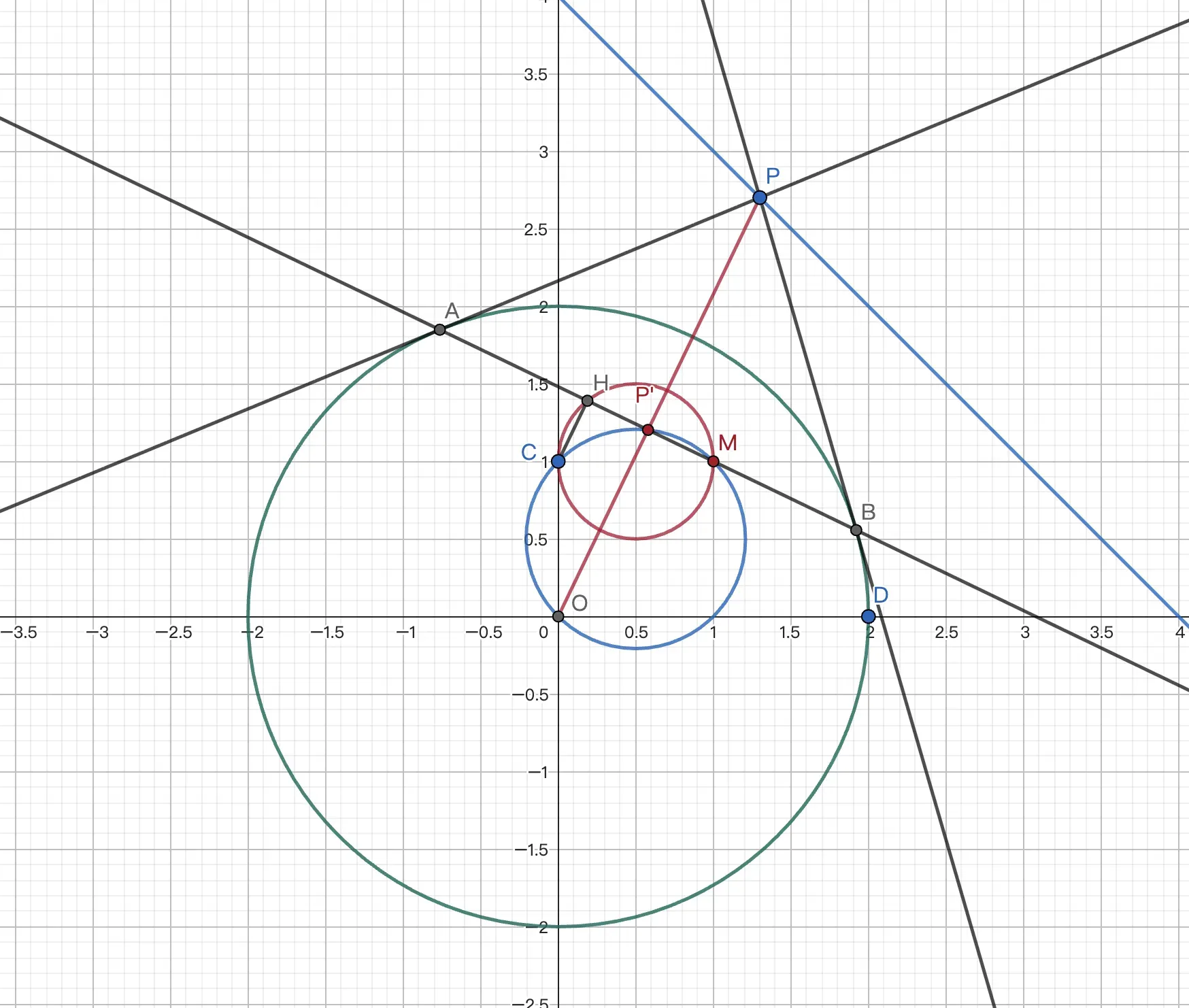
连 $OP$ 交 $AB$ 与 $P'$，则 $P'$ 是 $P$ 关于 $\odot C$ 的反演点. 故 $P'$ 轨迹为 $l$ 关于 $\odot C$ 的反形 $(x-\frac12)^2+(y-\frac12)^2=\frac12$. 由 $OP \bot AB$，可得 $AB$ 过 $O$ 的对顶点 $M(1,1)$. 又 $C(0,1)\bot AB$，有 $H$ 在以 $CM$ 为直径的圆上.

故 $DH\ge \frac{\sqrt{13}-1}2$.

调和类

例1 椭圆 $C:\frac{x^2}4+\frac{y^2}9=1$ 的左顶点为 $A$. 过点 $R(-2,3)$ 作直线 $l$ 交 $C$ 于 $P,Q$ 两点， $AP,AQ$ 交 $y$ 轴于 $M,N$. 求证：$MN$ 的中点在定点上.

解：

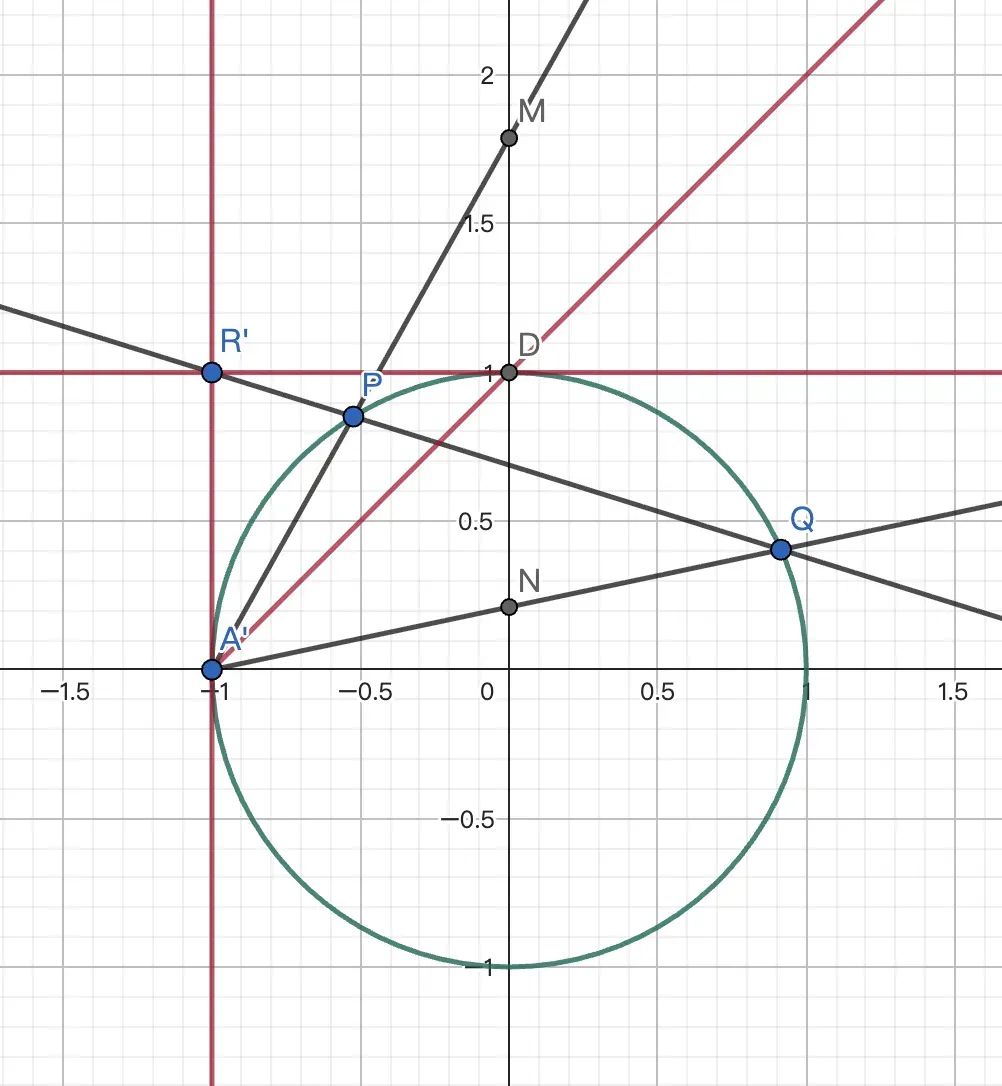
作仿射变换 $(x,y)\rarr(\frac{x}2,\frac{y}3)$， 使 得 $C\rarr\odot O:x^2+y^2=1,R\rarr R'(-1,1),A\rarr A'(-1,0)$. 作 $\odot O$ 顶点 $D(0,1)$，显然 $R'D,R'A'$ 是 $\odot O$ 的两条切线，所以四边形 $A'PDQ$ 是调和四边形，$A'R',A'M,A'D,A'N$ 是调和点列. 又 $A'R'\,//\,MN$，故 $D$ 是 $MN$ 中点.

回到原图，$MN$ 中点为定点 $(0,3)$.

例2 设 $P$ 是直线 $x=4$ 上异于 $(4,0)$ 的任意一点，斜率存在的 $AB$ 是经过椭圆 $\frac{x^2}4+\frac{y^2}3=1$ 右焦点 $F$ 的一条弦，记直线 $PA,PF,PB$ 的斜率依次为 $k_1,k_2,k_3$，求 $\frac{k_1+k_3}{k_2}$.

解：

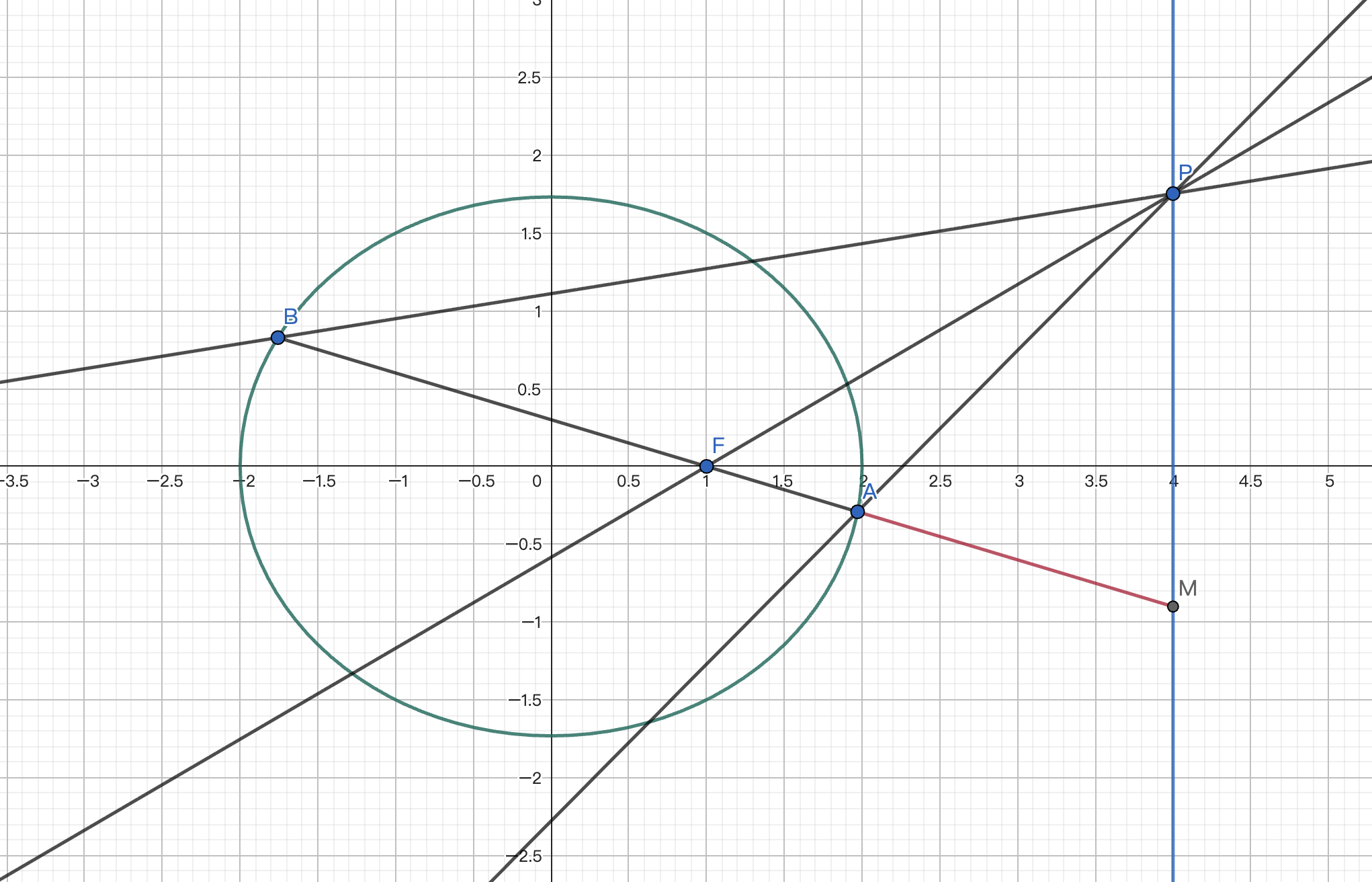
延长 $BA$ 交 $x=4$ 于 $M$，因为 $x=4$ 是 $F(1,0)$ 的极线，有 $F,M$ 共轭，则 $B,F,A,M$ 为调和点列，$PB,PF,PA,PM$ 为调和线束. 又 $x=4$ 垂直于 $x$ 轴，故有 $\frac{k_1+k_3}{k_2}=2$.

最后一步的证明是直截了当的，留给读者作为习题.

曲线系类

例1 已知双曲线 $C:x^2-\frac{y^2}{16}=1$，在 $x=\frac12$ 上取一点 $F$，过 $F$ 作直线 $l_0,l_1$ 分别交 $C$ 于 $A,B$ 和 $C,D$，有 $AF\cdot BF=CF\cdot DF$. 求 $k_{l_0}+k_{l_1}$.

解：

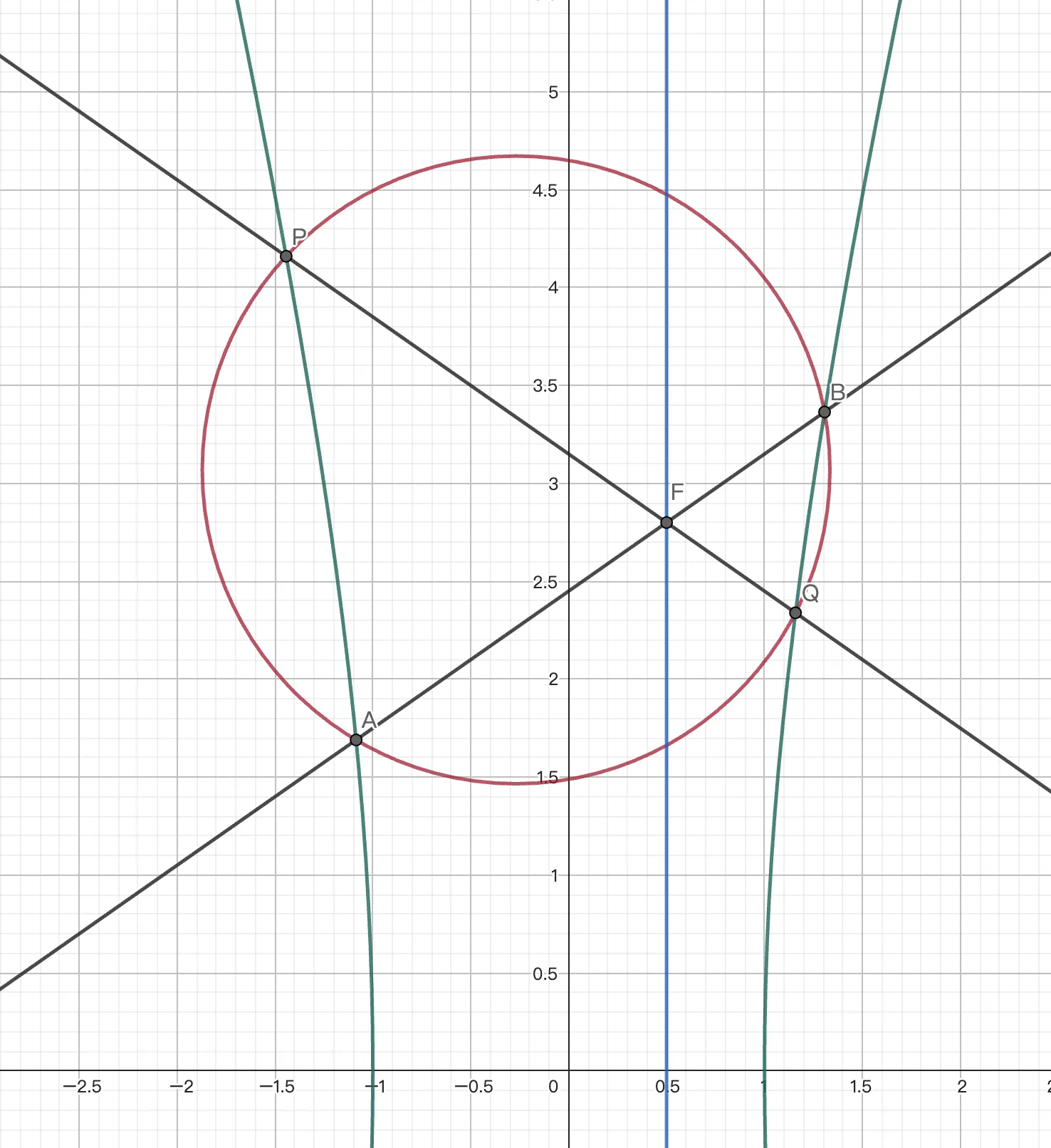
设 $l_0:y-k_0x+b_0=0,l_1:y-k_1x+b_1=0$，则 $l_0\cup l_1:(y-k_0x+b_0)(y-k_1x+b_1)=0$. 故过 $A,B,P,Q$ 的二次曲线系为 $D:\alpha (y-k_0x+b_0)(y-k_1x+b_1)+\beta(x^2-\frac{y^2}{16}-1)=0$.由圆幂定理，$A,B,P,Q$ 四点共圆，则存在 $\alpha,\beta$ 使得 $D$ 中 $x^2,y^2$ 项系数相等，且 $xy$ 项系数为 $0$，此时显然 $\alpha\neq 0$，因此 $k_0+k_1=0$.

面积类

例1 设抛物线 $C:y=\frac{x^2}4$，过点 $F(0,1)$ 作两条互相垂直的直线分别交抛物线于 $A,B$ 和 $D,E$，且 $A,E$ 在 $y$ 轴右侧，$B,D$ 在 $y$ 轴左侧. 作 $AB$ 中点 $M$ 和 $DE$ 中点 $N$. $AE$ 与 $BD$ 交于 $P$. 求三角形 $MPN$ 面积最小值.

解：

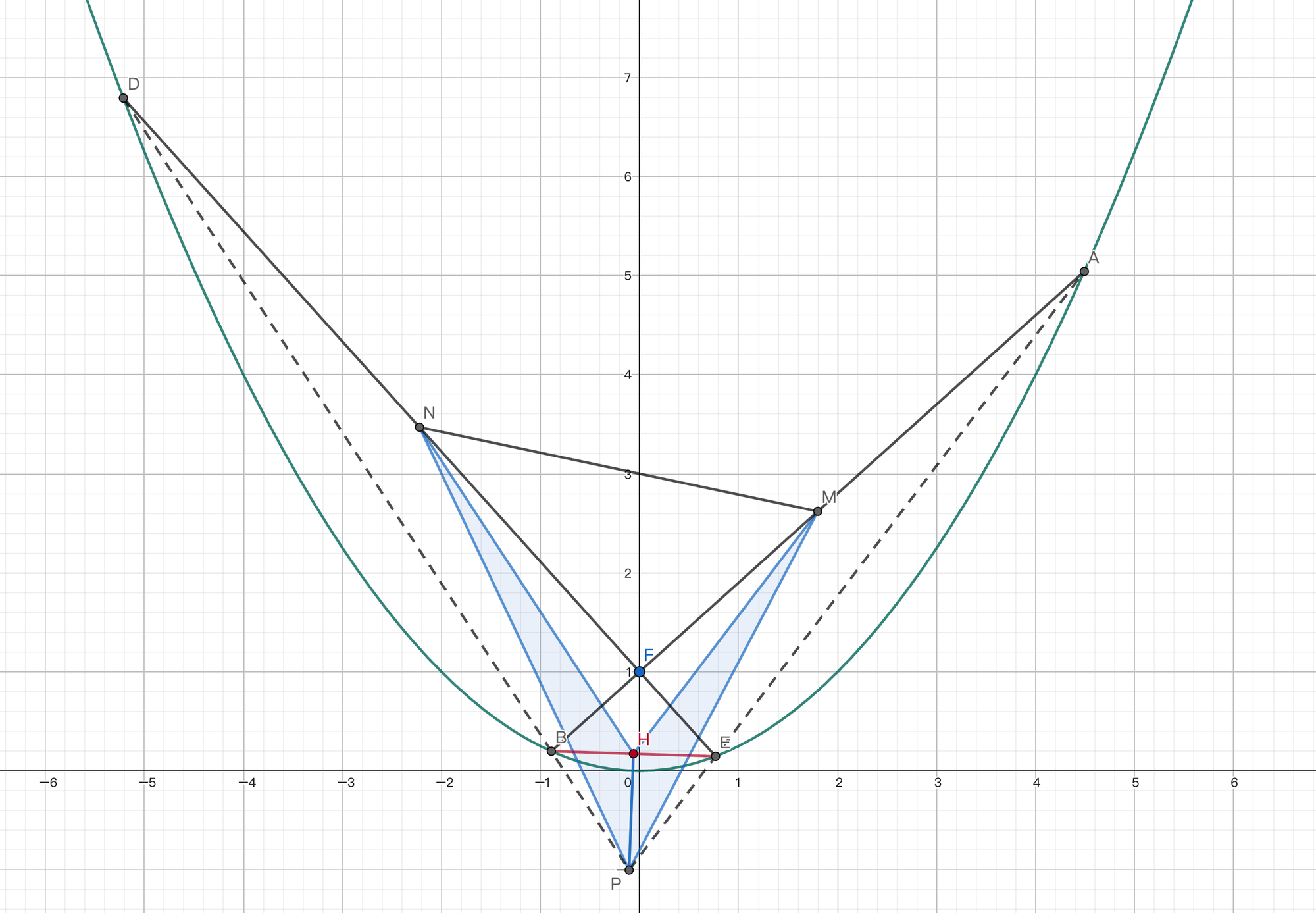
作 $BE$ 中点 $H$，由中位线可得 $MH\,//\,AP,NH\,//\,DP$. 于是 $S_{\triangle{MHP}}=S_{\triangle {MHE}},S_{\triangle{NHP}}=S_{\triangle{NHB}}$. 因此 $S_{\triangle{MPN}}=S_{\triangle{MFN}}+S_{\triangle{NHB}}+S_{\triangle{MHE}}=S_{四边形MNEB}=\frac12NE\cdot BM=\frac18AB\cdot DE$.

设 $AB:y=k_1x+1,DE:y=k_2x+1,k_1k_2=-1$. 联立 $C$ 和 $AB$，得 $X_A+X_B=4k_1,X_AX_B=-4$. 则 $AB=\sqrt{k_1^2+1}(X_A-X_B)=\sqrt{(k_1^2+1)[(X_A+X_B)^2-4X_AX_B]}=4(k_1^2+1)$. 同理得 $DE=4(k_2^2+1)$. 故 $S_{\triangle{MPN}}=2(k_1^2+1)(k_2^2+1)=2(k_1^2k_2^2+k_1^2+k_2^2+1)=2(k_1^2+\frac1{k_1^2}+2)=2[(k_1-\frac1{k_1})^2+4]\ge8$.

取 $k_1=1,k_2=-1$，面积为 $8$，故 $S_{\triangle{MPN}}$ 最小值为 $8$.

注意不到面积转化的话，强行计算也是可以得出结果的. 技巧如下：首先由极点极线结论有 $Y_P=-1$. 取 $Q(0,-1)$，注意在 $MN$ 斜率大于 $0$ 的时候，$X_P>0$，反之 $X_P<0$，因此总有 $S_{\triangle{MPN}}\ge S_{\triangle{MQN}}$. 改为求 $MQN$ 面积极小值可以极大简化计算.

原题抛物线为 $y^2=4x$，改为竖向是为了便于坑害初三的朋友们.

其他

例1 椭圆 $C:\frac{x^2}{16}+\frac{y^2}{12}=1$ 的左顶点为 $A$，右焦点为 $B$. 椭圆上有一点 $C$，$AC$ 与 $l_1:x=8$ 交于 $M$，过 $A$ 作 $MF$ 的平行线交 $CF$ 于 $R$. $x$ 轴上是否存在定点 $G$，使得 $\angle ARG=\angle FRM$ 恒成立？若有，求出 $G$ 坐标. 若无，请说明理由.

解：

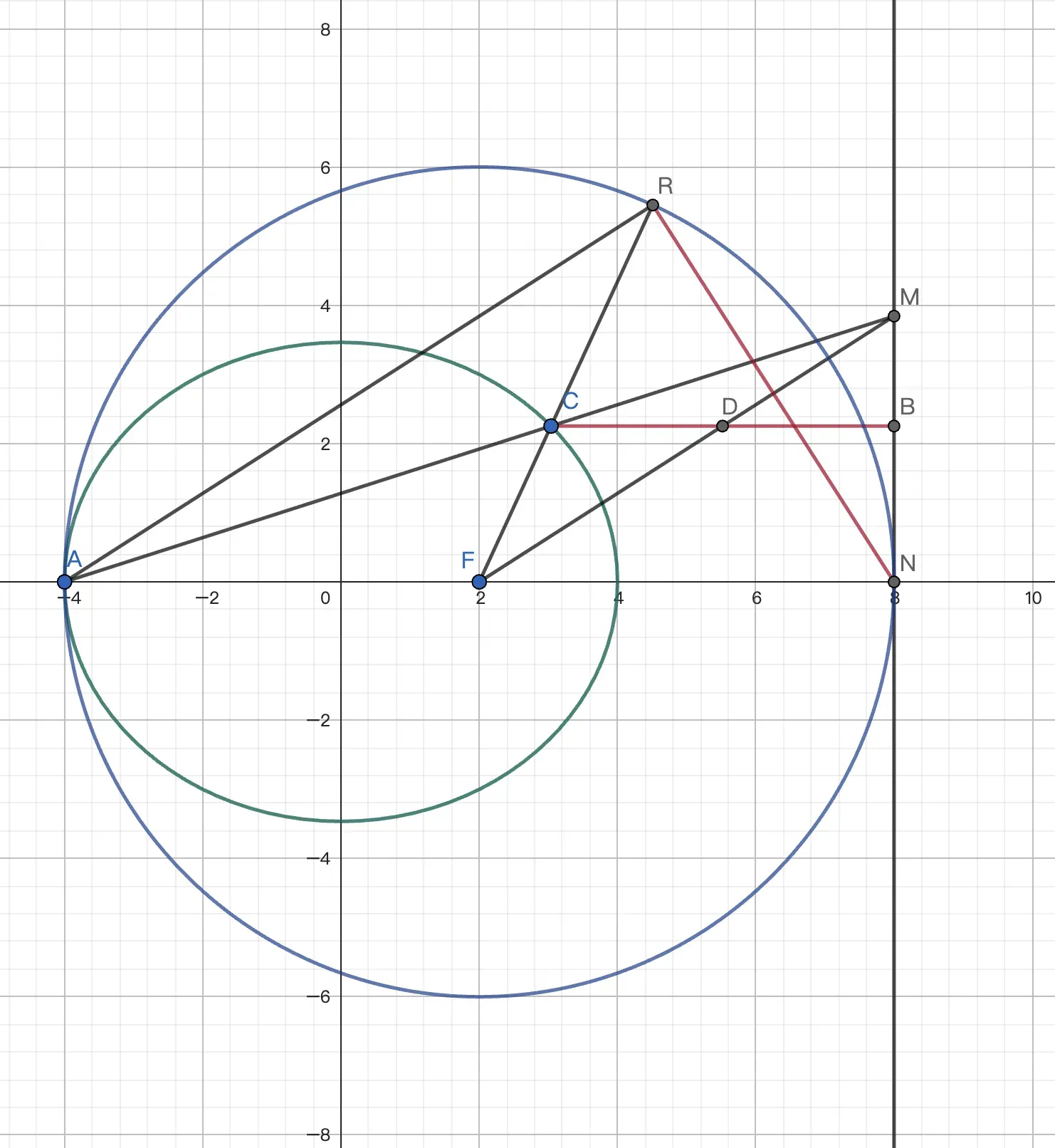
注意到 $l_1$ 是 $C$ 的右准线，设 $l_0$ 与 $x$ 轴交于 $N$. 作 $CB\bot l_0$，有 $CB=2CF$. 因为 $AF=FN$，由相似有 $DB=DC=CF$，故 $\angle CFD=\angle CDF=\angle MFN$. 因为 $AR\,//\,MF$，$\angle ARF=\angle RFM=\angle MFN=\angle RAF$，所以 $AF=FR=FN$，故 $R$ 在 $F$ 为圆心，$AF$ 为半径的圆上.由角平分线和切线，$\angle MRN=\angle MNR=\angle RAN=\angle ARF$，所以 $\angle ARN=\angle FRM$. 因此定点 $G$ 为 $N(8,0)$.

本做法需要注意到 $R$ 的轨迹，这几乎是不可能的，因此只能作为知晓答案后炫技式的娱乐. 但是证明过程的确相当漂亮，其中通过准线得出角平分线的方法是较为一般的，可以体会一下.

例2 椭圆 $C:\frac{x^2}8+\frac{y^2}2=1$ 过点 $A(2,1)$，$P,Q$ 是 $C$ 上的两个动点，使 $\angle PAQ$ 的角平分线垂直于 $x$ 轴，证明：$PQ$ 斜率为定值，并求出该值.

解：

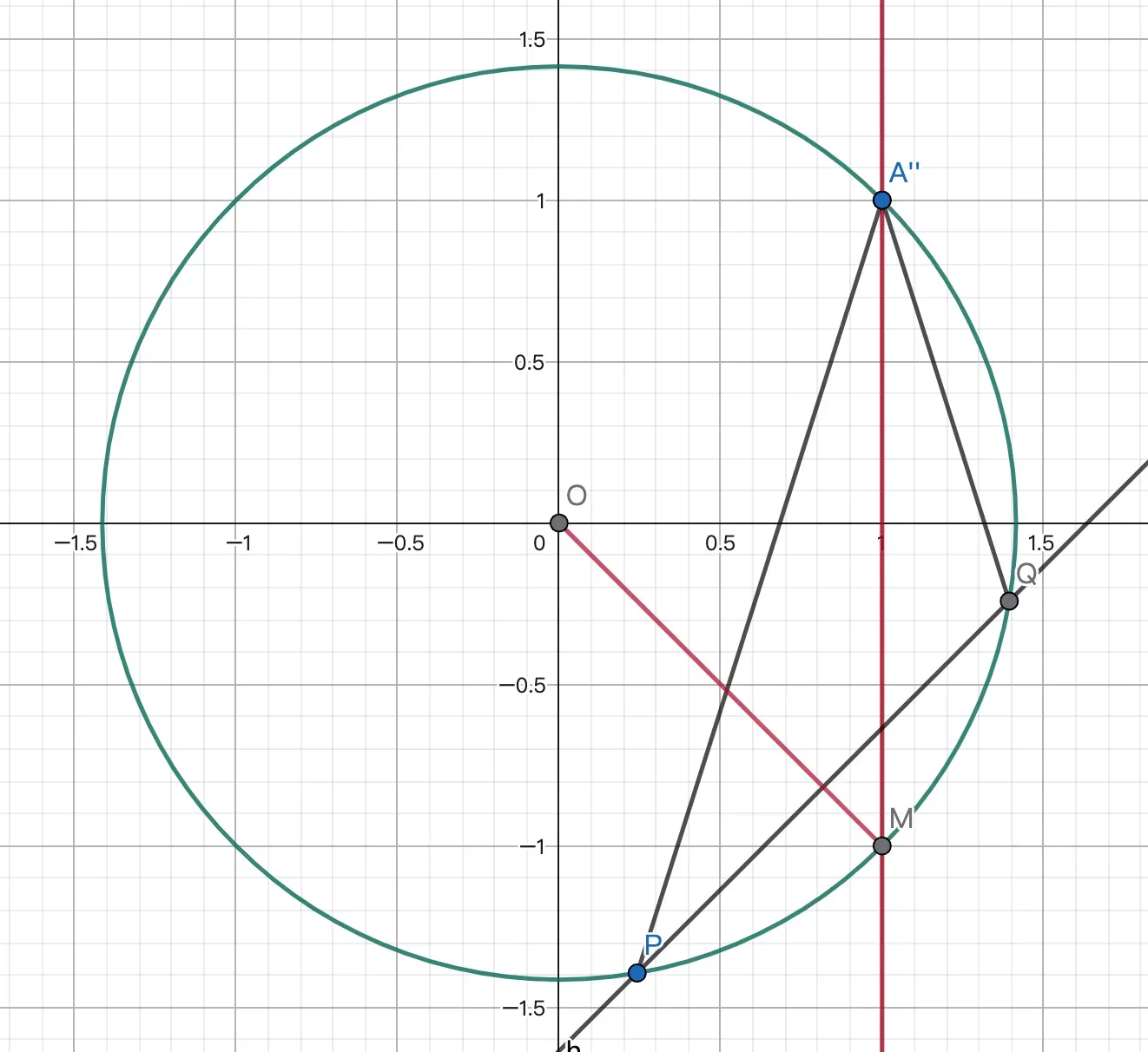
作仿射变换 $(x,y)\rarr (\frac x2,y)$，则 $C\rarr \odot O:x^2+y^2=1,A\rarr A'(1,1)$.作 $M(1,-1)$，则 $A'M$ 平分 $\angle PAQ$，有 $\overset{\frown}{PM}=\overset{\frown}{QM}$，因而 $OM\bot PQ$，所以 $k_{PQ}=1$.
回到原图，$k_{PQ}$ 为定值 $\frac12$.

例3 椭圆 $C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 内接四边形 $ABCD$ 对角线 $AC,BD$ 交于点 $P(1,1)$，且 $AP=2CP,BP=2DP$. 已知 $k_{AB}=-\frac14$，求椭圆的离心率.

解：

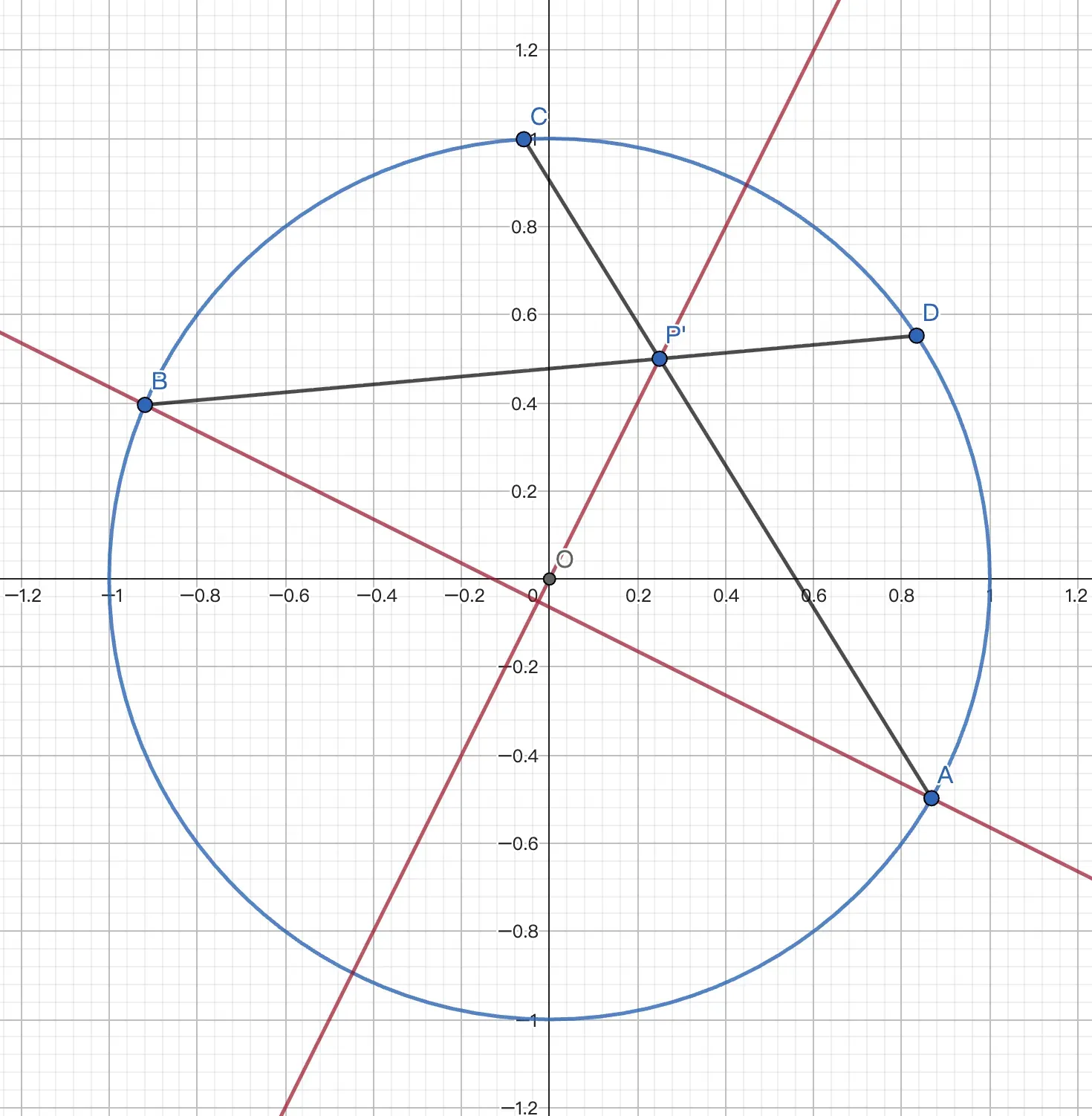
作仿射变换 $(x,y)\rarr(\frac x a,\frac y b)$，使得 $C\rarr \odot O:x^2+y^2=1,P\rarr P'(\frac1a,\frac1b),k_{AB}'=\frac a b k_{AB}=-\frac a {4b}$.因为 $\frac{AP'}{CP'}=\frac{BP'}{DP'}=2$，显然 $AC,BD$ 关于 $OP$ 对称. 故有 $OP'\bot AB$，从而 $k_{AB}'\cdot k_{OP}=-1$，解得 $a=2b$，故椭圆离心率为 $\frac{\sqrt3}2$.

例4 如图，圆 $O:x^2+y^2=4$ 的左右顶点为 $A,B$，过圆上一点 $C$ 作圆的切线交过 $A,B$ 的切线于点 $D,E$. $AE，BD$ 交于点 $M$，求 $M$ 点轨迹.

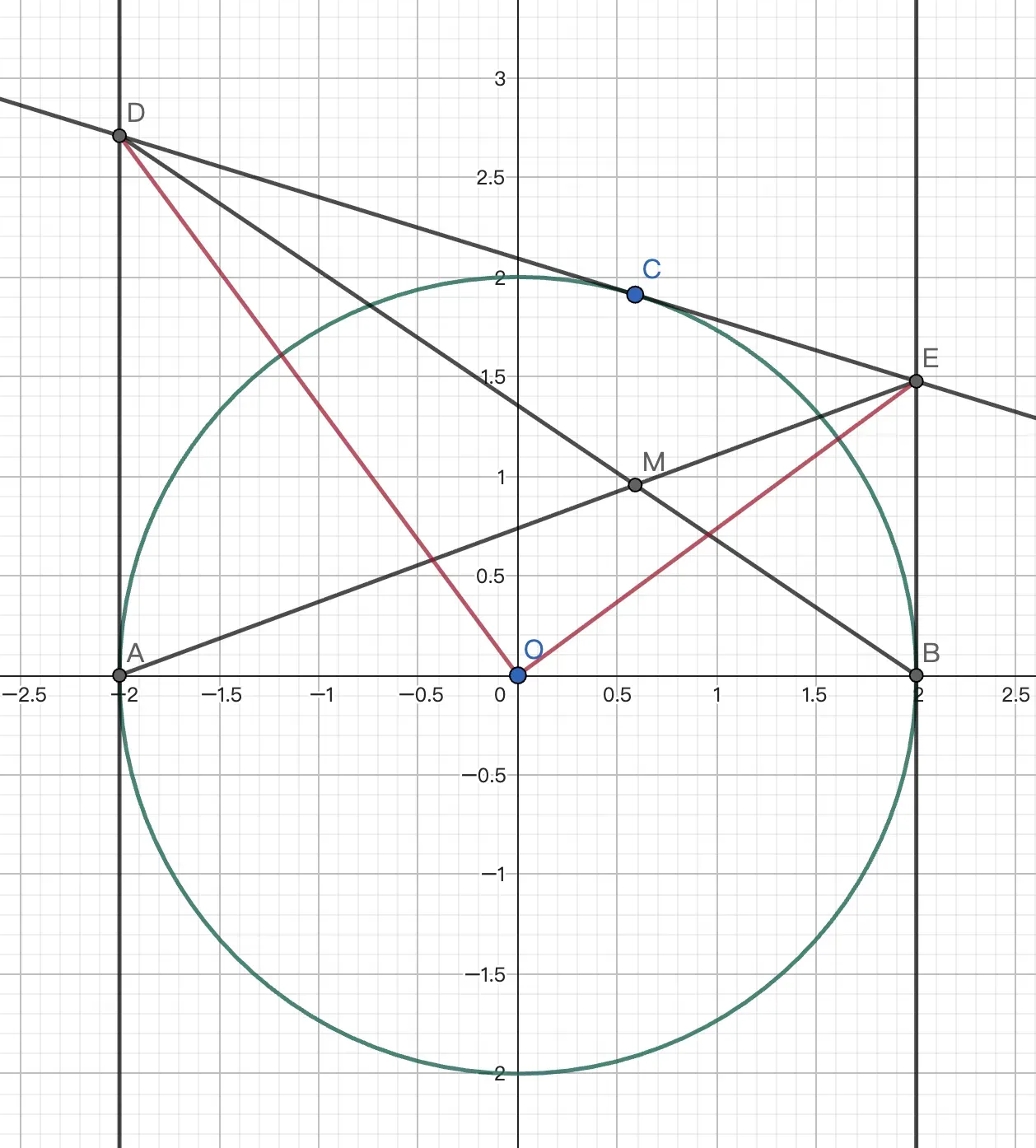
解：因为 $AB=2OB=2BA$，有 $k_{AE}=\frac12k_{OE},k_{BD}=\frac12k_{OD}$，所以 $k_{AE}\cdot k_{BD}=\frac14k_{OE}\cdot k_{OD}=-\frac14$.

由椭圆第三定义不难得到 $M$ 轨迹为 $\frac{x^2}4+y^2=1$.

例5 椭圆 $C:\frac{x^2}2+y^2=1$ 的左焦点为 $F_1$，直线 $y=kx$ 交 $C$ 与 $A,B$. 连结并延长 $AF_1,BF_1$ 交 $C$ 与 $D,E$. 求 $DE$ 斜率 $k_{DE}$ 与 $k$ 的关系.

解：

作仿射变换 $(x,y)\rarr(\frac{x}{\sqrt2},y)$，则 $C\rarr\odot O(x^2+y^2=1)$，$F_1\rarr F_1'(-\frac{\sqrt2}2,0)$.
设 $DE$ 交 $x$ 轴与 $M$，由坎迪定理有 $\frac1{MF_1'}-\frac1{r-OF_1'}=\frac1{OF_1'}-\frac1{r+OF_1'}$.所以 $MF_1'=\frac{\sqrt2}6$.设 $AB,DE$ 交于 $C$，则 $C$ 在 $F_1$ 的极线 $x=-\sqrt2$ 上. 设 $C(-\sqrt2,y_c)$，得 $k'=\frac{-y_c}{\sqrt2},k_{DE}'=\frac{-y_c}{\frac{\sqrt2}3}$，所以 $k_{DE}'=3k'$.

由于仿射变换前后直线斜率比不变，有 $k_{DE}=3k$.

例6 已知圆 $C_1:(x-1)^2+y^2=2$，圆 $C_2:(x-a)^2+(y-\sqrt2)^2=12$. 若圆 $C_1$ 上存在两点 $A,B$，且圆 $C_2$ 上恰好存在一点 $P$，使得四边形 $OAPB$ 为矩形，求实数 $a$ 的取值集合.

解：

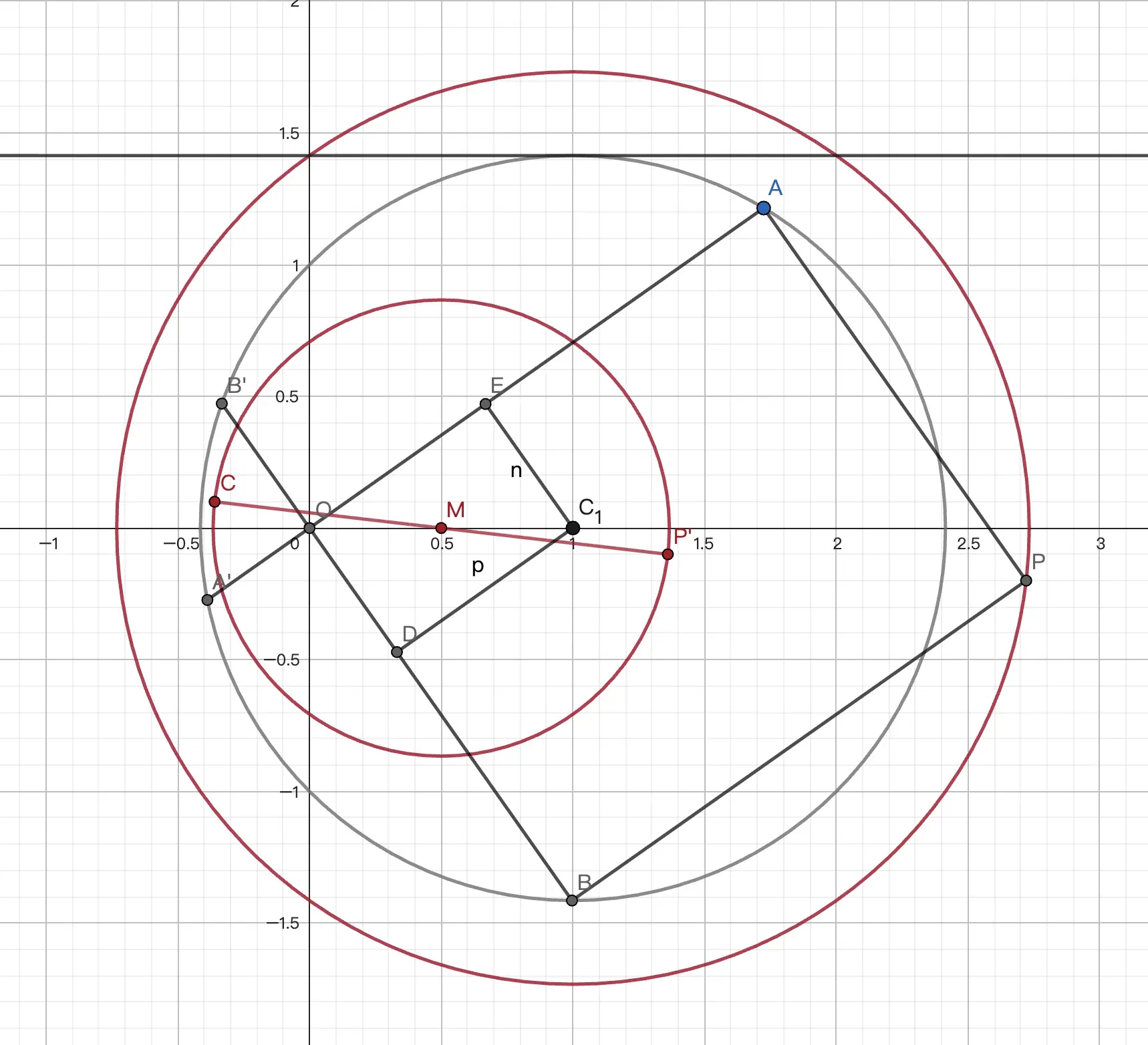
延长 $AO,BO$ 与圆 $C_1$ 交于点 $A',B'$. 取 $AB$ 中点 $P'$，$A'B'$ 中点 $C$. 连 $CP'$. 取 $AA',BB'$ 中点 $E,D$，易知 $C'P'$ 中点与 $ED$ 中点重合 (都为四边形 $ABA’B’$ 重心) ，记为 $M$. 由垂径定理和 $AO\bot OB$，四边形 $OEC_1D$ 为长方形. 故 $M$ 为 $CC_1$ 中点.又 $CP'^2=(\frac{AA'}2)^2+(\frac{BB'}2)^2=AE^2+BD^2=AC_1^2-C_1E^2+BC_1^2-C_1D^2=2r_{C_1}^2-ED^2=2r_{C_1}^2-CC_1^2=3$. 所以 $MP'=\frac{\sqrt3}2$. 即 $P'$ 在 $M$ 为圆心，$\frac{\sqrt3}2$ 为半径的圆上.

因为 $CP'=PP'$，故 $P$ 在 $C_1$ 为圆心，$\sqrt3$ 为半径的圆上.

由于 $C_2$ 恰有一个点 $P$ 满足条件，有 $C_2$ 与 $C_1$ 相切. 易得 $a\in\{-4,0,2,6\}$.