奔驰定理的三维推广

设空间中一点 $H$ 和四面体 $ABCD$ 满足 $a\overrightarrow{HA}+b\overrightarrow{HB}+c\overrightarrow{HC}+d\overrightarrow{HD}=0$，其中 $a,b,c,d$ 全不为 $0$. 求证：$V_{H-BCD}:V_{H-ACD}:V_{H-ABD}:V_{H-ABC}=|a|:|b|:|c|:|d|$.

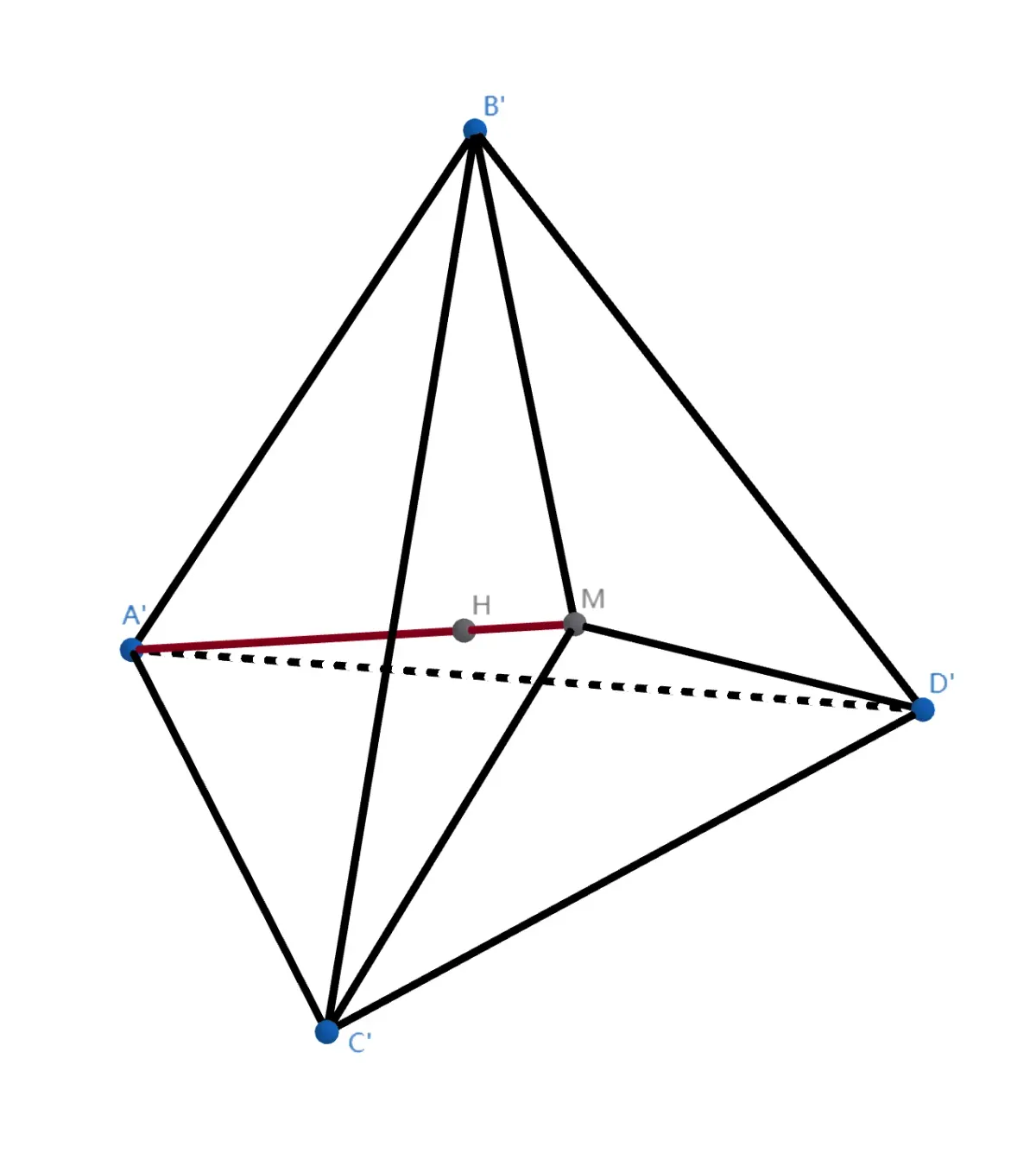
证明 设 $\overrightarrow{HA'}=a\overrightarrow{HA},\overrightarrow{HB'}=b\overrightarrow{HB},\overrightarrow{HC'}=c\overrightarrow{HC},\overrightarrow{HD'}=d\overrightarrow{HD}$，则有 $\overrightarrow{HA'}+\overrightarrow{HB'}+\overrightarrow{HC'}+\overrightarrow{HD'}=0$.

设 $M$ 为 $B'C'D'$ 重心，则 $\overrightarrow{HM}=\frac13(\overrightarrow{HB'}+\overrightarrow{HC'}+\overrightarrow{HD'})=\frac13\overrightarrow{A'H}$. 所以 $A',H,M$ 三点共线. 又 $S_{\triangle B'C'M}=S_{\triangle B'D'M}=S_{\triangle C'D'M}$，有 $V_{H-A'B'C'}=V_{H-A'B'D'}=V_{H-A'C'D'}$.

由对称性，$V_{H-A'B'C'}=V_{H-A'B'D'}=V_{H-A'C'D'}=V_{H-B'C'D'}$.

由 $V_{H-ABC}=\frac{V_{H-ABC}}{V_{H-ABC'}}\cdot\frac{V_{H-ABC'}}{V_{H-AB'C'}}\cdot\frac{V_{H-AB'C'}}{V_{H-A'B'C'}}\cdot V_{H-A'B'C'}=\frac{HC}{HC'}\cdot\frac{HB}{HB'}\cdot\frac{HA}{HA'}\cdot{V_{H-A'B'C'}}=\frac{1}{|abc|}V_{H-A'B'C'}$. 同理可得 $V_{H-ABD}=\frac{1}{|abd|}V_{H-A'B'D'},V_{H-ACD}=\frac{1}{|acd|}V_{H-A'C'D'},V_{H-BCD}=\frac{1}{|bcd|}V_{H-B'C'D'}$.

故 $V_{H-BCD}:V_{H-ACD}:V_{H-ABD}:V_{H-ABC}=|a|:|b|:|c|:|d|$. 命题得证.